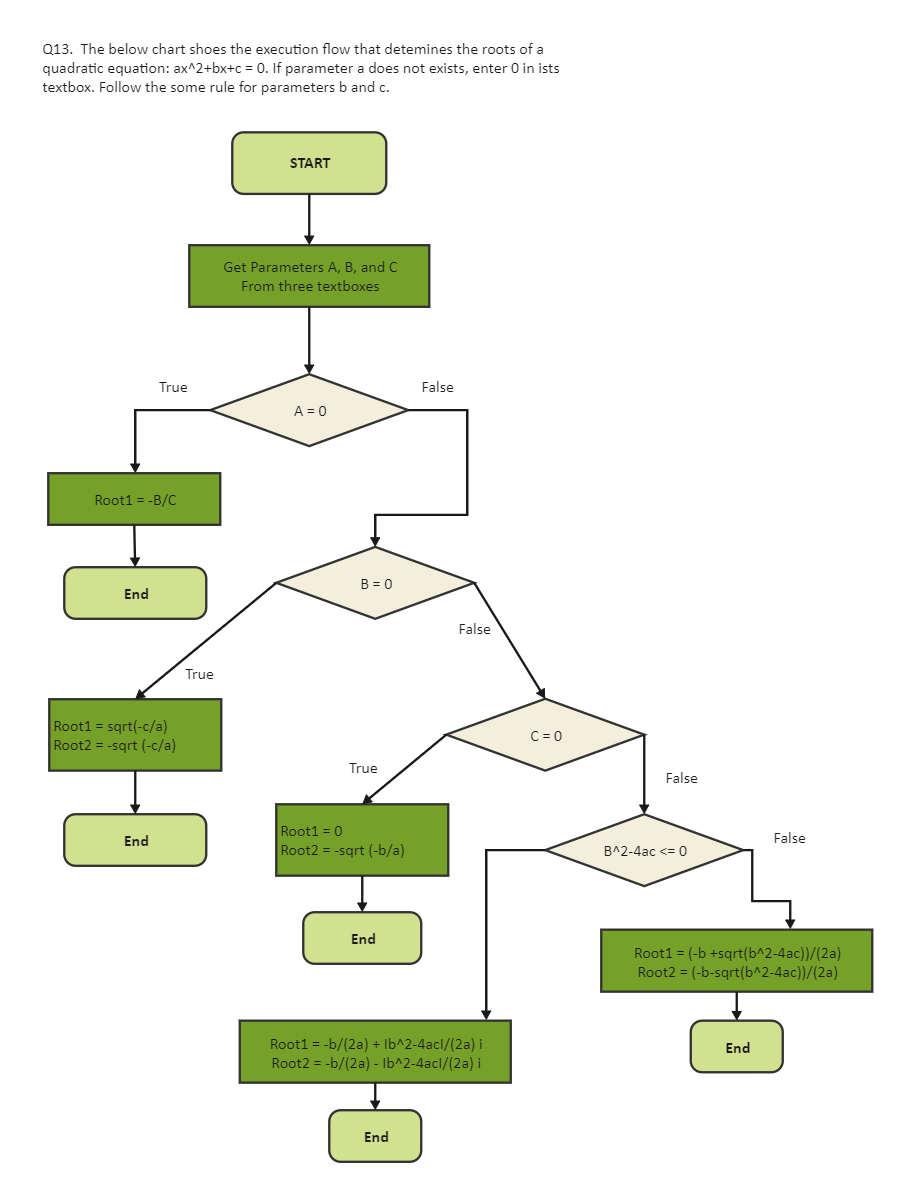
A quadratic equation is an equation in the form of ax^2 + bx + c = 0, where a is not equal to zero. The roots of the quadratic are the numbers that satisfy the quadratic equation. There are always two roots for any quadratic equation, although sometimes they may coincide. The algorithm diagram below shows that the quadratic form of ax^2 + bx + c replaces them with 0. This is done because the roots of the equation are the values where the y-axis is equal to zero. For instance, get parameters A, B, and C, and if A = 0, then the Root 1 = -B/C, else we will have to see if B is equal to zero. If B=0 then Root1 = sqrt (-c/a) and Root2 = -sqrt(-c/a). But if C=0 then Root 1 will also be equal to zero and Root2 = -sqrt (-b/a).
