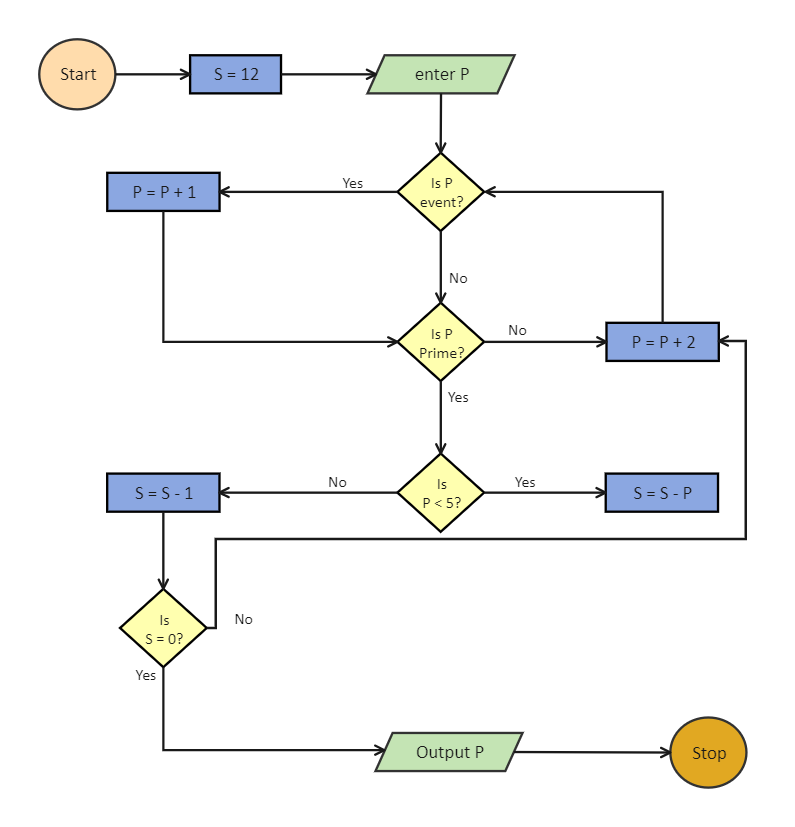
To prove whether a number is a prime number, first try dividing it by two and see if you get a whole number. If you do, it cannot be a prime number. If you do not get a whole number, try dividing it by prime numbers: 3, 5, 7, 11, and so on, constantly dividing by a prime number. To understand this mechanism, one can create an algorithm. As shown in the below algorithm, the process starts by assigning S a value of 12 and then entering the P. If P is an even number, then increase P by one. If the new value of P is a prime and is less than five, then the new value of S becomes S-1. Else the new value of S = S - P. If the new value of S comes equal to zero, then the machine should print the value of P and stop the algorithm, else increase the value of P by P+2 and see if the new value of P is divided by two or not.
