A Guide to Understand Parabolic Curve with Diagram
In mathematics, parabolic curves are necessary geometric figures. They are used in the graphical representation to understand the correlation between two factors. Other than that, architecture, physics also use properties of parabolic curves. Starting from the shape of a banana to the movement of a bullet or a ballistic missile, one can observe parabolic curves in multiple places. Therefore, the students should be aware of the parabolic curves. It will help them study some crucial concepts related to engineering, architecture, physics, and maths.
1. The Parabolic Curve
According to mathematics, a plane curve with a U shape with a mirror-symmetry is a parabolic curve. A parabola has a point which is called a focus and a directrix. Any point present on the directrix line is equidistant from the focus of the parabola. A plane, positioned parallelly, with one side of the cone will help to create a parabolic shape. The intersection of the cone and the plane represents the parabolic curve.
In parabolic curve representation, consider the X-axis and Y-axis. The shape of curves on both sides of the Y-axis is the same. They are like mirror reflections. This property of the parabolic shape is known as symmetry.
The Y-axis is the axis of symmetry, in the case of the graphical representation of a parabola. The vertex of the parabolic shape is named the (0,0) point, with x=0 and y=0.
1.1 Reflector
The parabolic reflector devices are mainly like mirrors and possess reflective properties. They have the property with which they can collect electromagnetic rays like light at a single focal point. The parabolic reflector can also form parallel rays in case the point source is lying at the focus.
The use of parabolic reflectors is increasing rapidly. One can witness the modern usage of the principle of parabolic reflectors is there in dish antennas. The device behaves like a parabolic reflector as it sends and receives signals.
1.2 Equation
Mathematically, quadratic functions can represent a parabola having the highest power of pro-numeral in terms of two. Students can represent a parabolic curve with a general equation. y = a(x-h)2 + k or x = a(y-k)2 +h. In this equation, h and k are the vertices. Hence, represent a regular parabola with the equation y2 = 4ax.
The equation of parabola can be represented in various ways:
- y2= 4ax
- y2= - 4ax
- x2= 4ay
- x2 = - 4ay
The students will have a parabolic shape when values are put in this equation and plotted in a graph.
1.3 Examples
There are several examples of the parabolic shape. The trajectory of ballistic missiles, bridges, and arches, and radar dishes are parabolic in shape. Many constructions use the features of parabolic curves to even out the stress on them.
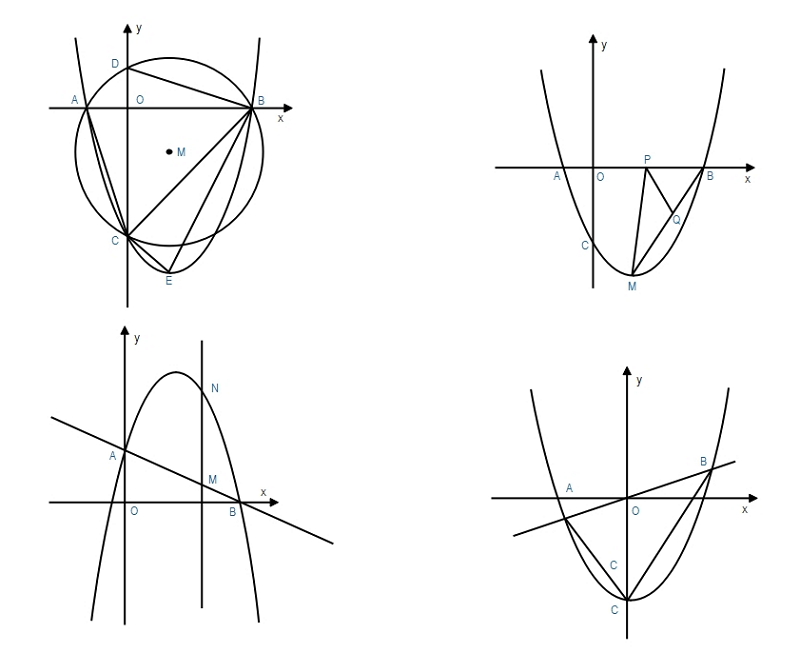Source:EdrawMax Online
2. How to Draw the Parabolic Curve?
When a student is studying physics and maths, there are instances when they must learn the parabolic curve. However, creating a perfect parabolic curve can be difficult. It can be time-consuming, and the students may fail to generate a high-quality result.
2.1 How to Create Parabolic Curve from Sketch
To create a parabolic curve by hand, the students must follow these steps:
Step 1: To create a parabolic curve, the students can use graph paper. After that, they need to position the same. If a student has selected a rectangular-shaped paper, they can keep its long side at the top. To avoid this confusion regarding positioning, the students can use square graph paper.
Step 2: After that, the students need to make a straight line joining the left corner of the first cube of the top row to the right corner of the first cube of the bottom row. Next, they have to join the left corner of the first cube of the second row to the right corner of the last cube of the second column. The students need to continue this process.
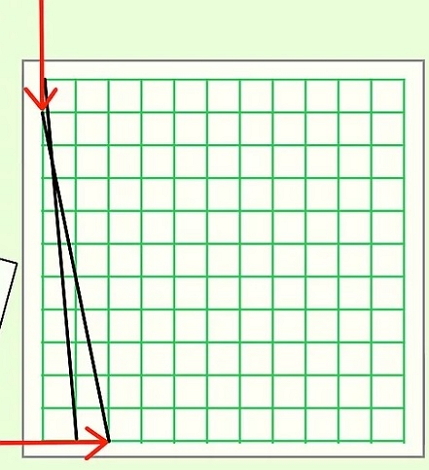
Step 3: The students have to join the lines till the end of the page. They need to make sure that they are connecting the correct points. A mistake in the same may result in a change in shape.
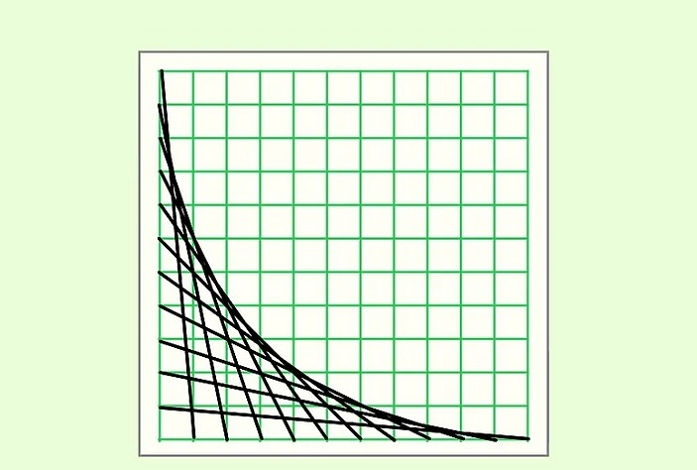
This process is complicated, and there are ample chances for a student to join the wrong points.
2.2 How to Create Parabolic Curve Online
If the students don't use graph paper and create evenly-spaced points with the help of a ruler, the drawing can be more challenging and time-taking. To avoid such conditions, the students must use the EdrawMax Online tool. It is a user-friendly tool, and many users consider it as their trusted diagramming companion.
The tool has more than 25 million users and is apt for creating more than 260 different types of diagrams. Here are a few simple steps which the students need to follow to draw a parabolic curve diagram on the EdrawMax online tool:
Step 1: EdrawMax Online comes with an easy-to-use interface. It has become a favorite of the students and the individuals who need to work with charts and diagrams. The students can use EdrawMax Online without any experiencing of using an online tool. To start with the process, the students need to open the EdrawMax Online tool. Then they need to open New.
Step 2: The students need to find the Science and Education option. They can use this tool to study multiple education and science-related topics with the help of these diagrams. To get the parabolic curve diagram, the students must go to the ‘Mathematics’ option. Under this option, they can find the parabolic curve.
Step 3: Once the student has selected the parabolic curve diagram, they can modify it according to their requirements. They can use this perfect parabolic curve diagram for their lessons, projects, and dissertation papers.
Step 4: After editing the diagram, the students can save the same in multiple formats and then export it to use in the future. The tool is accessible from several devices and is fit to use in different operating systems. Thus, the students can also access the EdrawMax online tool from any device and work anytime and anywhere.
3. Parabolic Curve Examples
There are numerous parabolic curves examples scattered in nature. Many artificial wonders are based on parabolic curves. Here are a few examples of parabolic curves :
- Bridges and Arches
- Dish Antennas
- Roller Coaster
One can observe the parabolic curves in cable-tie bridges. They are generally U-shaped, and the structure that supports the whole body of the bridge also has a parabolic shape. Arches are classic architectural examples of parabolic curves.
Their shape does not only make them look magnificent but allows them to equalize the stress by compressing it on the outside and downwards.
The dish antennas need to conduct the signal by maintaining a connection between the source and the receiver. It has the shape of a parabolic curve, which improves its directivity and makes it easier to receive the signal.
A roller coaster has multiple ups and downs, turns, and twists. The curves of the roller coasters have the shape of the parabolic curves.
4. Conclusion
To study architecture, physics, and Maths, the students must have a complete idea about the calculations and equations related to the parabolic curves. For that, the students can take the help of a parabolic curve diagram. However, it is tough to create a parabolic curve diagram by hand. To save time, the students must use the EdrawMax online tool.
In conclusion, EdrawMax Online is a quick-start diagramming tool, which is easier to make parabolic curves and any 280 types of diagrams. Also, it contains substantial built-in templates that you can use for free, or share your science diagrams with others in our template community.
