Venn Diagram Symbols and Set Notation
1. Set Notation
As the basic of venn diagram symbols, set notation is used in mathematics to define the set type and its properties. The set notation uses a system of symbols to:
- Define the properties of elements in a set.
- Show the relationships among sets.
- Show operations among sets.
The set notation in Venn diagram has some specific rules for describing a set. It uses curly brackets or braces { }, and the members of the set called elements are placed in these curly braces, which are sometimes referred to as braces. The names of the sets are denoted by capital English letters usually.
Source: EdrawMax Commnutiy - Venn Diagram Symbols
Some examples of sets in set notations are as follows.
- Set of natural numbers: N = {1, 2, 3, 4, 5...}
- N = the set of natural numbers greater than or equal to 1.
- N = {n | n ∈ ℕ, n ≥ 1}
- {} curly brackets is the set symbol to limit the set description
- ∈ = element of a set
- ∉ = 'is not a member of' or 'is not an element of.'
- | and: can be used to show "where" or "such that"
- ⊂ : subset
- ⊄ : is a set symbols to show it is not a subset
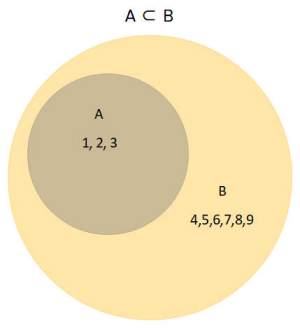
For example, if all the elements of set A are also members of set B, then we can say that A ⊂ B.
If A = {1, 2, 3} and B = {1,2,3,4,5,6,7,8,9}
Then A ⊂ B i.e. 'A is a subset of B'.
2. Venn Diagrams Symbols Explained
In set theory, many operations can be performed on given sets. These operations can be represented with Venn diagram symbols. Venn diagrams are effective tools for describing the set theory operations visually. Though there are around 30 Venn diagram symbols, the most important are discussed below.
- Union of Set
- Intersection of set
- Complement of set
- Difference of set
2.1 Union of two sets: ∪ symbol
In a Venn diagram, each circle represents a particular set or category. The ∪ symbol in math represents the union of two sets or two circles eventually. In a two-circle Venn diagram, the complete diagram illustrates the operation A ∪ B. A ∪ B means a set of all members of A or B or both.
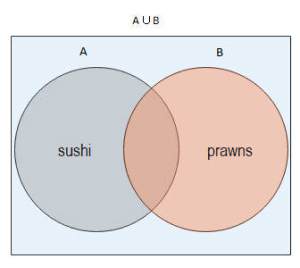
For example, set A may represent people who like sushi, and set B may portray people who want to eat prawns. So, A ∪ B may represent people who like sushi, prawns, or both.
2.2 The intersection of two sets: ∩ symbol
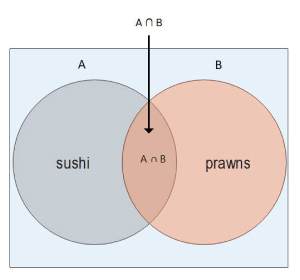
The intersection of two sets is represented by the Venn diagrams symbol ∩. An intersection set has all the members common in both sets or categories. In the Venn diagram, the intersection is the area overlapped by both circles.
So, if A represents people who like sushi and B has people who want to eat prawns. So, the A ∩ B set contains all people who like both sushi and prawn.
2.3 Complement of a set: Ac
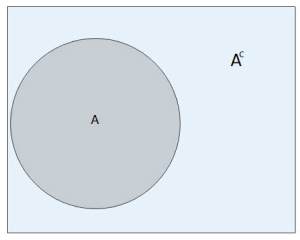
When you want to represent what is not represented in a set, every member that is not included in set A is the complement of set A, Ac. It represents members that are not present in set A and can be represented using a Venn diagram with a circle. If the letter U represents the Universal set, then the region covered in the universal set, excluding the area covered by set A, represents the complement of A.
2.4 Difference of Set Venn Diagram
The difference of sets or relative complement of a set is represented by the Venn diagram symbol operation A - B. A-B has all the members of A which do not belong to B. In a Venn diagram, circles show A-B as the region covered by set A, excluding the area that is common to set B
2.5 Empty Set
The empty set can be denoted by the Venn diagram symbol "Φ" and "φ" or { }. The empty set is a set with no elements.
2.6 Universal Set
A universal set is a set containing all relevant members from the perspective of a problem under consideration. The universal set symbol is the capital letter U . A universal set includes everything you are interested in or everything that is relevant to the problem you have.
3. Three or More Sets in a Venn Diagram
Three sets Venn diagrams or 3-circle Venn diagrams consist of three overlapping circles to show the relationship between the elements of three sets. Many connections exist in a three-set Venn diagram. If A, B, and C are three circles in Venn Diagram, then we can observe;
- Members common in A and B = Members in A and B only plus elements in A, B, and C.
- Members common in B and C = Members in B and C only plus elements in A, B, and C.
- Members common in A and C = Members in A and C only plus elements in A, B, and C.
Let us explain this with the following example.
| Animal | A | B | C |
| Dog | x | ||
| Tiger | x | ||
| Giraffe | x | x | x |
| Ant | x | ||
| Cow | x | x |
Venn Diagram area for A U B shows {Dog, Giraffe, Cow, Tiger}
Venn Diagram for A U B U C shows {Dog, Giraffe, Cow, Tiger, Ant}
Venn Diagram for A ∩ C shows {Giraffe}
Source: EdrawMax Online
4. Tips for Using Venn Diagram Symbols
Venn diagrams are very useful in many fields. Mathematicians use them to solve complex problems. These diagrams help in the organization of information and to represent relationships for visual communication.
Here are some tips for using Venn diagram symbols for your requirements.
- It is important that you know the basic goal and expected output from your Venn diagram. It sets a firm base for the efficient and effective use of your chart. Understand your goal. It is always helpful to have a statement of your basic intent ready before starting the actual drawing.
- Next, carefully and correctly pick up your sample. It may look simple for trivial examples, but for complex systems, the sample determination needs proper analysis and observation. You should be able to think out of the box and understand the difference between observations, choices, arguments, or decisions.
- Once your groundwork is done, determine your Venn Diagram style. You may refer to the templates library in EdrawMax to review different samples and techniques of Venn diagrams.
- Find Venn diagram symbols quickly from EdrawMax Online>Symbol Library> Smart Shapes>Venn chart.
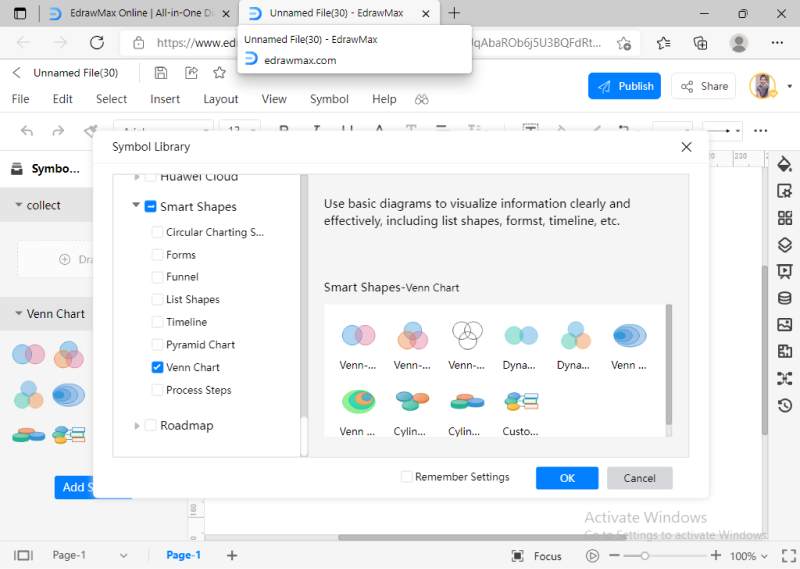
- EdrawMax Online has a comprehensive symbols library, but if you do not find your required Venn diagram symbol, you can also import symbols as images, symbols, or data from files format such as SVG, VSSX, and so on. Go to the library option on the sidebar and click on the import icon. A new pop-up window will appear, allowing you to import your files.
EdrawMax Online is a premium drawing software with comprehensive symbols, an easy-to-use layout, and an exclusive collection of templates. You can use this program easily using the following tips to save time and effort.
You can also learn more from this video. YouTube.
5. Conclusion
Venn diagrams are visual representations of set theory concepts from mathematics. They use specific Venn diagram symbols to show logical relationships between different groups of sets. These diagrams can be very helpful in probability theory, logic and statistics, mathematics and computer science, linguistics, sociology, and marketing. EdrawMax Online is a powerful Venn diagram maker with an exhaustive library for UML symbols and also for other 280+ diagram types. You can also use the free and fully customizable professional Venn diagram examples available in the template community. Many general scenarios are already available in the templates community so that you can start fast on a firm foundation.
Edraw.AI
